コラム
Column
周波数・変位・速度・加速度の基礎
「周波数」「変位」「速度」「加速度」は、振動を制御するための基本となる4つの要素です。
本コラムでは、それぞれの意味と互いの関係性について解説します。
「周波数」・「変位」・「速度」・「加速度」とは
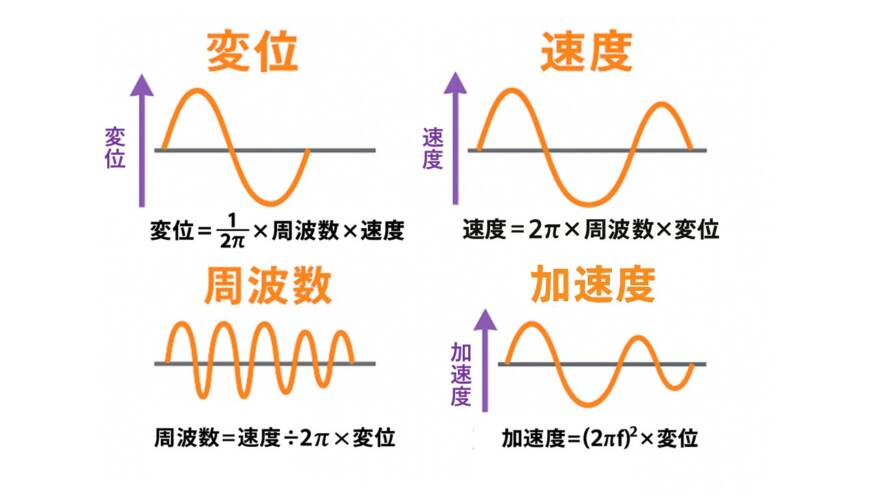
■ 周波数(Frequency) 単位:Hz(ヘルツ)
🔹意味:振動が1秒間に何回繰り返されるかを表す値
🔹単位:ヘルツ(Hz)
🔹使い方の例:振動試験で「30Hz」の設定なら、1秒間に30回揺れていることを意味します。
📌ポイント:周波数が高いほど「細かく・速く」揺れる。
■ 変位(Displacement) 単位:mm(ミリメートル)
🔹意味:振動によって位置がどれだけ移動したか(振幅)
🔹単位:ミリメートル(mm)など
🔹使い方の例:上下に±1mm動くなら、変位は2mm(両振幅p-p)または1mm(片振幅0-p)と表現されます。
📌ポイント:変位が大きいほど「揺れ幅が広い」。
■ 速度(Velocity) 単位:m/s(メートル毎秒)
🔹意味:振動中の移動スピード(動く速さ)
🔹単位:メートル毎秒(m/s)またはミリメートル毎秒(mm/s)
🔹使い方の例:振動試験において、速度は「単位時間あたりの変位の変化量」として定義されます
📌ポイント:速度は「2π×周波数×変位」で決まり、周波数または変位が大きいほど速く動く。
■ 加速度(Acceleration) 単位:m/s²(メートル毎秒毎秒)
🔹意味:速度がどれくらい急に変化するか(振動の力の強さ)
🔹単位:m/s² または 重力加速度を基準とした「G(ジー)」
🔹使い方の例:振動試験で「3G」の設定は、地球の重力の3倍の力が加わっていることを意味します。
📌ポイント:加速度は「(2πf)²×変位」で計算できます。
要約
| 項目 | 簡単な説明 | 増加するとどうなる? |
| 周波数 (Hz) | 1秒間に何回揺れるか | 1秒間に振動する回数が増える為、振動が細かく・速くなる |
| 変位 (mm) | どれだけ大きく揺れるか(振れ幅) | 揺れ幅が大きくなる(大きく動く) |
| 速度 (mm/s) | 振動中の動くスピード | 移動スピードが速くなる |
| 加速度 (m/s²・G) | 振動の勢い(強さ) | 衝撃や振動が強くなるため、試験品に大きな力がかかる |
「周波数」「速度」「変位」「加速度」の相互関係
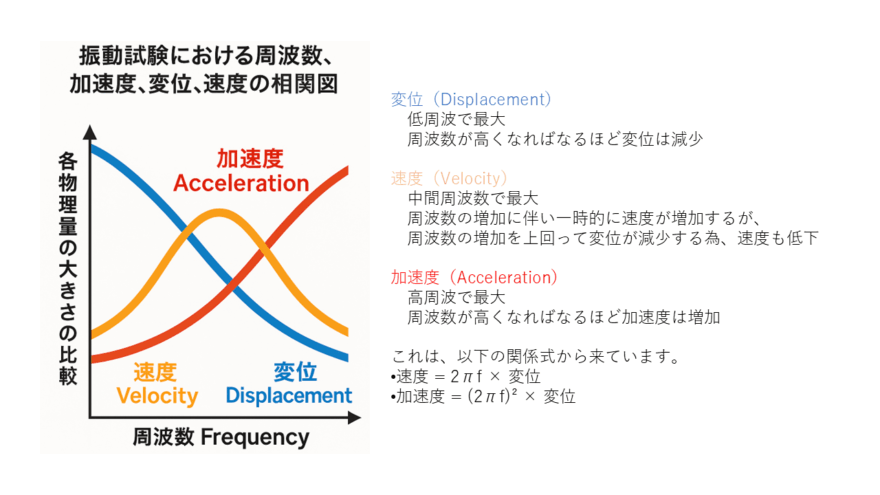
周波数(Hz)が変わるとどうなる?
周波数が上がる=1秒間に振動する回数が増える
変位が同じでも、より短い時間で行ったり来たりするため、
速度が速くなる
加速度はもっと大きくなる
✅ 例:変位が1mmで一定のとき
- 10Hz → ゆっくり揺れる(速度も加速度も小さい)
- 50Hz → 細かく速く揺れる(速度も大きく、加速度はかなり大きく)
変位(mm)が変わるとどうなる?
変位が大きくなる=揺れ幅が広がる(動きが大きい)
周波数が一定でも、
速度が速くなる(広い距離を同じ時間で動くため)
加速度も大きくなる(移動距離が増えるぶん、力も強く必要)
✅ 例:周波数が20Hzで一定のとき
- 変位1mm → コンパクトな動き、力も小さい
- 変位5mm → 大きく揺れて、速度も力も大きい
速度(mm/s)が変わるとどうなる?
速度が速くなる = 単位時間あたりに動く距離が大きい(動きが速い)
周波数や変位のいずれか、または両方が大きくなると速度が増す
✅ 例:加速度が一定のとき
- 速度が遅い(周波数が低い、変位が大きい) → なだらかな動き
- 速度が速い(周波数が高い、変位が小さい) →素早い動き
加速度(m/s², G)が変わるとどうなる?
加速度が大きくなる = 動きの変化が急になり、衝撃が強くなる(瞬間的な力が増す)
特に周波数の2乗に比例するため、周波数が高いと影響が大きくなる。
✅ 例:速度が一定のとき
- 加速度が小さい(周波数が低い)→ ゆっくりなめらかな動き、衝撃は弱い
- 加速度が大きい(周波数が高い)→ 急激で鋭い動き、 衝撃が強くなる
まとめ
本記事では、振動試験における4つの基本パラメータ――周波数・変位・速度・加速度――の関係性とそれぞれの意味について解説しました。
これらは個別に理解するだけでなく、相互の関連性を把握することで、より的確な試験設定が可能になります。
弊社では、試験条件の検討やご相談も承っております。
試験試験に関するご相談がございましたら、ぜひお気軽にお問い合わせください。







